MATEMATIKO

for
MIDDLE SCHOOL, GED,  ASVAB

MATH PREPARATION CLASSES

OVERVIEW

Designed for teachers and students to offer extra practice in the basic skills.  It can be used as an independent instructional tool in conjunction with a manual such as the popular GED math manuals available at most bookstores.  It is best used, however, as an instructional tool in GED preparation and middle school classes.    Examples are generated by the program in a random fashion.  This means that there are an unlimited number of unique examples available. Results can be printed out.  Another feature of the program is that when a student makes a mistake, the program will not allow a student to continue making mistakes until the problem is successfully corrected.  In a classroom environment this encourages students to figure out the answer or to ask the teacher for help.

Before purchasing, consider the following:

• Program does not include word problems at this time.
• Meant as a practice program to be used with a tutor or manual.
• Includes over 100 modules.
• Unlimited number of examples.
• Developer is available to help users solve the examples via email.
• Program will help users learn multiplication facts.
• A checklist to measure progress is available on line.

CONTENT OF PROGRAM

Practice sessions on the following topics:

1. Learn Multiplication Tables – Speed Mode

2. Learn Multiplication Tables – Practice Mode

3. Multiplication Tables – Test Mode

4. Learn Addition Tables – Speed Mode

5. Learn Addition Tables – Practice Mode

6. Addition Tables – Test Mode

7. Learn Subtraction Tables – Speed Mode

8. Learn Subtraction Tables – Practice Mode

9. Subtraction Tables – Test Mode

10. Learn Division Tables – Speed Mode

11. Learn Division Tables – Practice Mode

12. Division – Test Mode

13. Basic Addition – no carry

14. Basic Addition – easy

15. Basic Addition – intermediate

16. Basic Addition – hard

17. Basic Addition – columns

18. Basic Subtraction – no borrow

19. Basic Subtraction – easy

20. Basic Subtraction – intermediate

21. Basic Subtraction – hard

22. Basic Subtraction – from zeros

23. Basic Multiplication – easy

24. Basic Multiplication – intermediate

25. Basic Multiplication – hard

26. Basic Multiplication – times ten

27. Basic Multiplication – times mult ten

28. Basic Division – easy

29. Basic Division – intermediate

30. Basic Division – hard

31. Basic Division – divide by ten

32. Average (mean)

33. Median

34. Reduce Fractions

35. Adding Fractions with Common Denominators

36. Adding Fractions with Different Denominators

37. Subtracting Fractions with Common Denominators

38. Subtracting Fractions with different Denominators

39. Multiplication of Fractions

40. Division of Fractions

41. Reduce Mixed Numbers

42. Addition of Mixed Numbers

43. Subtraction of Mixed Numbers

44. Multiplication of Mixed Numbers

45. Division of Mixed Numbers

46. Basic Decimal Addition – easy

47. Basic Decimal Addition – intermediate

48. Basic Decimal Addition – hard

49. Basic Decimal Subtraction – easy

50. Basic Decimal Subtraction – intermediate

51. Basic Decimal Subtraction – hard

52. Basic Decimal Multiplication – easy

53. Basic Decimal Multiplication – intermediate

54. Basic Decimal Multiplication – hard

55. Basic Decimal Multiplication – times ten

56. Basic Decimal Division – easy

57. Basic Decimal Division – intermediate

58. Basic Decimal Division – hard

59. Basic Decimal Division – by ten

60. Fractions to Decimals

61. Solve Proportions

62. Percents – find part

63. Percents – find whole

64. Percents – find percent

65. Percents – mixed types

66. Powers and Roots – basic powers

67. Powers and Roots – basic roots

68. Powers and Roots – advanced powers

69. Powers and Roots – advanced roots

70. Powers and Roots – third power

71. Probability Demonstration

72. Interest formula

73. Distance formula

74. Total Cost formula

75. Distributive Property

76. Order of Operations

77. Number Series

78. Simple Addition Equations

79. Simple Subtraction Equations

80. Mixed Addition and Subtraction Equations

81. Simple Multiplication Equations

82. Simple Division Equations

83. Mixed Multiplication and Division Equations

84. Simple Two-step Equations

85. Equations with Parentheses

86. Equations with Separated Unknowns

87. Add Signed Numbers

88. Subtract Signed Numbers

89. Multiply Signed Numbers

90. Divide Signed Numbers

91. Perimeter of Square

92. Area of Square

93. Perimeter of Rectangle

94. Area of Rectangle

95. Perimeter of Triangle

96. Area of Triangle

97. Area of Circle

98. Circumference of Circle

99. Pythagorean Relationship

100. Area of Parallelogram

101. Angles of Triangles

102. Angles formed by transversal of Parallel lines.

OVERVIEW OF TABLES MODULES

These modules offers three learning modes --- test mode, practice mode, and speed mode.  With each mode or menu selection, the learner can choose multiplication, division, addition, or subtraction. The test mode is an inventory of the 81 basic multiplication, addition, subtraction, and division facts. This is used to obtain a baseline and for students who already have a good mastery and wish to improve it. In the practice mode, the student chooses a table that he has a problem with for extra practice. The speed mode is similar to the practice mode, but it encourages speed.

When a student has completed, he or she has the opportunity to review the results.   A printed copy of the results can be made for the teacher's records.

TABLES TEST MODE

gives the student a baseline with which to compare progress. Eighty-one basic examples (multiplication, subtraction, division, or addition) are given in a random fashion. That is, no two tests will have the examples in the same order.  When an example is answered correctly, the display is shown in blue.   When there is an error, the display turns red.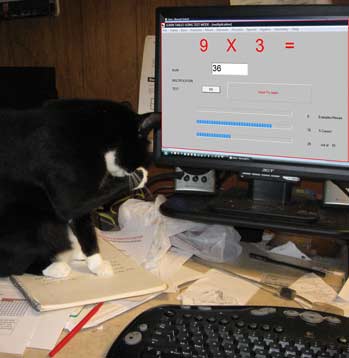

On the screen, a student sees three bars.

1. Progress bar. Shows number of examples completed.
2. Accuracy bar. Keeps a running tally of the percent of correct answers.
3. Speed bar. Indicates the speed the students are correctly completing the examples.

When completed, the student can print out the results.  This includes the percent correct and the duration of the test. The printout also includes a bar graph showing which tables the student needs to work on in the practice or speed modes.

 TABLES PRACTICE MODE

is used it to practice individual tables. For example, if the chart from the test indicates that a student needs practice with the nines tables. The student will select table nine and the number of examples desired. The developer usually instructs his students to select 50 examples. Fifty examples will then be randomly selected. There will naturally be repeats, but this will help learning.  When an example is answered correctly, the display is shown in blue.  When there is an error, the display turns red.

The bars found in the test mode above are also used in this mode:

1. Progress bar. Shows number of examples completed.
2. Accuracy bar. Keeps a running tally of the percent of correct answers.
3. Speed bar. Indicates the speed the students are correctly completing the examples.

When completed, the student can print out the results.  This includes the percent correct. The printout also includes a bar graph showing which examples the student needs to work on in the practice or speed modes.

 SPEED MODE

encourages students to be quick when practicing. Students can determine how long he or she needs to complete each problem from 2 to 9 seconds. Students should be encouraged to use this mode to increase their speed and accuracy.

This mode works like the practice mode with a few differences. Like the practice test, the student will select a table he or she is having a problem with and like the others, the figures remain blue if the answer is correct and turn red when an error is made. A feature unique to this mode is that after a delay ,selected by the student, the display turns green. The student can choose from one second to nine seconds. The object therefore is not only to come up with the correct response, but to come up with the correct response within two seconds.

A second difference between this mode and the practice mode is that when an example is answered correctly and accurately, it is not again bdisplayed on the screen for the current session. This is similar to using flash cards.  When a math fact is memorized it is taken out of the pack of flash cards.

PROBABILITY DEMO

Graphically shows the outcomes when one die or two dice are rolled ten million times.  Can be used after students are given the opportunity to roll their own dice.  Good for probability and ratio exercises.  The developer gives each student two dice and graph paper to graph the results of rolling dice.  The students’ results often look very much like the results on the computer screen.  Differences can be explained by the fact that probability is more accurate at ten million rolls.  How long would it take a person to roll dice ten million times? How long does it take the computer?

WHOLE NUMBERS

Practice adding, subtracting, multiplying, and dividing whole numbers of varying levels of difficulty.  Positive reinforcement is used.  The student knows immediately if he is correct or not.  If the example is incorrect, the screen text turns red.  He is not allowed to continue until he has a correct answer.  The student is given the opportunity to choose the number of examples and the level of difficulty.  The number of examples correct the first time around is given at the end of the exercise.

Also special modules are included such as:
Adding and subtracting without regrouping. (Sometimes needed for students with poor skills)
Subtracting where there are several 0 digits in the minuend.  (Many students need practice with this type of example.
Multiply by 10, 100. (To encourage students to do this type of problem without pencil and paper)

DECIMALS

Practice adding, subtracting, multiplying, and dividing decimal numbers of varying levels of difficulty.  Positive reinforcement is used.  The student knows immediately if he is correct or not.  If the example is incorrect, the screen text turns red.  He is not allowed to continue until he has a correct answer.  The student is given the opportunity to choose the number of examples and the level of difficulty.  The number of examples correct the first time around is given at the end of the exercise.

This section includes fraction to decimal conversion.  The student selects a denominator family.  The example are given in order from smallest fraction to largest.  For example if the 5 family is selected.  The examples given will be 1/5, 2/5, 3/5 etc.  This will help the students see the relationship between fractions and decimals.  The instructor can use this to encourage students to memorize some families, such as the thirds and fourths.

VERSION 2.05

·        The program runs on MICROSOFT WINDOWS. 

·   The program is shipped on one CD.

Number of visitors since June 4, 2007: 

This page updated June 4, 2007